Supongo que, a estas alturas, el lector está legitimado para pedir a quien esto escribe alguna prueba de que lo que está contando funciona en la práctica.
—Usted verá, lleva seis capítulos dando la turra con microorganismos, estrategias evolutivas, teoría de juegos y competiciones de ordenador y aún no sabemos dónde quiere ir usted a parar.
—Quiero ir a parar al punto de demostrar que existe un derecho natural inscrito en nuestros genes y que es producto de muchos millones de años de procesos evolutivos.
—Pues bien fácil lo tiene usted, pónganos un ejemplo de un caso en que la percepción innata de justicia del ser humano choque frontalmente con sus criterios racionales.
—Usted lo ha querido ¿conoce el «juego del ultimátum»?
—No.
—Pues vamos a él.
En el juego del ultimátum compiten dos jugadores y es un juego que sólo se juega una vez. Insisto. Este juego sólo se juega una vez y no perder esto de vista es esencial.
A uno de los dos jugadores (le llamaremos oferente) se le ofrece una cantidad de dinero, pongamos por ejemplo mil euros, y se le pide que, de esa cantidad, ofrezca a su contrincante una parte.
El jugador oferente puede ofrecer a su contrincante (llamémosle Respondedor) la cantidad que desee, desde los mil euros a un solo euro, pero (aquí está el pero) los jugadores solo podrán quedarse con el dinero si el Respondedor acepta la cantidad que se le ofrece, si no la acepta ambos lo oerderán todo.
Ahora reflexione y piense si usted fuese el oferente qué cantidad ofrecería y si fuese el respondedor con qué cantidad estaría dispuesto a conformarse, mientras yo le voy contando algunas cosas.
Desde el punto de vista económico y dado que el juego sólo se juega una vez las matemáticas nos dicen que el respondedor debe aceptar cualquier oferta superior a cero que le haga el oferente. Rechazar cualquier oferta superior a cero supone perder dinero sin contraprestación alguna, de forma que la lógica, la racionalidad económica y las matemáticas nos indican que la conducta racional para el respondedor es aceptar cualquier cantidad.
Sin embargo usted y yo sabemos que los seres humanos no somos así de racionales.
He hecho esta prueba con varios alumnos en prácticas en mi despacho y recuerdo con especial cariño una ocasión en que un joven abogado particularmente ágil de mente ofreció de los mil euros tan solo cinco a otra compañera abogada.
Esta miró con cara de estupor al oferente y este, viendo que ella iba a rechazar la oferta se le adelantó y le dijo:
—Piénsalo, es mejor cinco euros que nada.
Ella respondió
—¿Y el gusto que me va a dar a mí verte perder 995€? ¿Tú sabes cuánto vale eso, pedazo de gomias?
La compañera quizá no actuase racionalmente pero es así como funciona el ser humano. Una pulsión (emoción) construida durante millones de años de historia evolutiva humana la impulsaba a decirle a su competidor que de ella no se iba a reír.
Podemos especular qué habría ocurrido si la oferta, en vez de cinco hubiese sido de 495€. ¿Habría rechazado en tal caso la oferta la compañera? También podríamos especular sobre otras circunstancias pero lo cierto es que el ser humano, dentro de determinados límites, prefiere satisfacer una cierta pulsión de justicia a un simple beneficio económico aunque ello le lleve a comportarse irracionalmente.
Y ahora yo debería extenderme sobre las causas de esta particular forma de conducta del ser humano, de esta intuitiva percepción de lo justo y de lo injusto y de cómo, dentro de ciertos límites, el ser humano prefiere seguir sus instintos que la racionalidad. Pero eso lo haré en los próximos capítulos, en este prefiero escucharles a ustedes por si tienen algo que decir.
Para poder sostener que la justicia y el derecho surgen entre las sociedades de seres vivos como consecuencia de procesos naturales, es preciso antes exponer siquiera sea de forma somera qué son la teoría de la evolución y la teoría de juegos.
No me detendré ahora a explicar la teoría de la evolución —lo haré más adelante desde un enfoque «informacional»— pues, aunque sea superficialmente, es relativamente conocida. Sí lo haré, en cambio, respecto de la teoría de juegos ya que, en conversaciones con otros juristas, he detectado que es para ellos una absoluta desconocida. A explicar de forma somera qué es la teoría de juegos y un ejemplo clásico de la misma, va destinado éste post.
La teoría de juegos es un área de la matemática aplicada que utiliza modelos para estudiar interacciones en estructuras formalizadas de incentivos (los llamados juegos) y llevar a cabo procesos de decisión. Sus investigadores estudian las estrategias óptimas así como el comportamiento previsto y observado de individuos en juegos. Desarrollada en sus comienzos como una herramienta para entender el comportamiento de la economía, la teoría de juegos se usa actualmente en muchos campos, desde la biología a la filosofía y también (¿por qué no?) el derecho. Experimentó un crecimiento sustancial y se formalizó por primera vez a partir de los trabajos de John von Neumann y Oskar Morgenstern, antes y durante la Guerra Fría, debido sobre todo a su aplicación a la estrategia militar. En otras palabras, estudia la elección de la conducta óptima cuando los costes y los beneficios de cada opción no están fijados de antemano, sino que dependen de las elecciones de otros individuos.
El ejemplo que más a menudo suele usarse para ilustrar la teoría de juegos es el llamado “Dilema del prisionero” que, en su versión más clásica, es enunciado así (wikipedia):
La policía arresta a dos sospechosos. No hay pruebas suficientes para condenarlos y, tras haberlos separado, los visita a cada uno y les ofrece el mismo trato. Si uno confiesa y su cómplice no, el cómplice será condenado a la pena total, diez años, y el primero será liberado. Si uno calla y el cómplice confiesa, el primero recibirá esa pena y será el cómplice quien salga libre. Si ambos permanecen callados, todo lo que podrán hacer será encerrarlos durante seis meses por un cargo menor. Si ambos confiesan, ambos serán condenados a seis años.
Lo que puede expresarse como
Tabla de pagos 1
Vamos a suponer que ambos prisioneros son completamente egoístas y su única meta es reducir su propia estancia en la cárcel. Como prisioneros tienen dos opciones: cooperar con su cómplice y permanecer callados o traicionar a su cómplice y confesar. El resultado de cada elección depende de la elección del cómplice. Desafortunadamente, uno no conoce qué ha elegido hacer el otro. Incluso si pudiesen hablar entre sí, no podrían estar seguros de confiar mutuamente.
Si uno espera que el cómplice escoja cooperar con él y permanecer en silencio, la opción óptima para el primero sería confesar, lo que significaría que sería liberado inmediatamente, mientras el cómplice tendrá que cumplir una condena de 10 años. Si espera que su cómplice decida confesar, la mejor opción es confesar también, ya que al menos no recibirá la condena completa de 10 años, y sólo tendrá que esperar 6, al igual que el cómplice. Si, sin embargo, ambos decidiesen cooperar y permanecer en silencio, ambos serían liberados en sólo 6 meses.
Confesar es una estrategia dominante para ambos jugadores. Sea cual sea la elección del otro jugador, pueden reducir siempre su sentencia confesando. Por desgracia para los prisioneros, esto conduce a un resultado regular, en el que ambos confiesan y ambos reciben largas condenas. Aquí se encuentra el punto clave del dilema. El resultado de las interacciones individuales produce un resultado que no es óptimo -en el sentido de eficiencia de Pareto-; existe una situación tal que la utilidad de uno de los detenidos podría mejorar (incluso la de ambos) sin que esto implique un empeoramiento para el resto. En otras palabras, el resultado en el cual ambos detenidos no confiesan domina al resultado en el cual los dos eligen confesar.
Si se razona desde la perspectiva del interés óptimo del grupo (de los dos prisioneros), el resultado correcto sería que ambos cooperasen, ya que esto reduciría el tiempo total de condena del grupo a un total de un año. Cualquier otra decisión sería peor para ambos si se consideran conjuntamente. A pesar de ello, si siguen sus propios intereses egoístas, cada uno de los dos prisioneros recibirá una sentencia dura.
El científico cognitivo Douglas Hofstadter observó que la matriz de pagos del dilema del prisionero puede, de hecho, escribirse de múltiples formas, siempre que se adhiera al siguiente principio:
T > R > C > P
donde T es la tentación para traicionar (esto es, lo que obtienes cuando desertas y el otro jugador coopera); R es la recompensa por la cooperación mutua; C es el castigo por la deserción mutua; y P es la paga del primo (esto es, lo que obtienes cuando cooperas y el otro jugador deserta).
En el caso del dilema del prisionero, la fórmula se cumple: 0 > -0,5 > -6 > -10 (en negativo pues los números corresponden a años de carcel).
Las fórmulas anteriores aseguran que, independientemente de los números exactos en cada parte de la matriz de pagos, es siempre «mejor» para cada jugador desertar, haga lo que haga el otro.
Siguiendo este principio, y simplificando el dilema del prisionero obtendremos la siguiente matriz de pagos canónica para el dilema, esto es, la que se suele mostrar en la literatura sobre este tema:
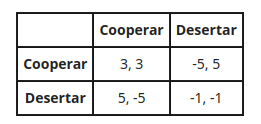
Tabla de pagos 2
En terminología «ganancia-ganancia» la tabla sería similar a esta:
Tabla de pagos 3
Estos ejemplos en concreto en los que intervienen prisioneros, intercambio de bolsas y cosas parecidas pueden parecer rebuscados, pero existen, de hecho, muchos ejemplos de interacciones humanas y de interacciones naturales en las que se obtiene la misma matriz de pagos. El dilema del prisionero es por ello de interés para ciencias sociales como economía, ciencia política y sociología, además de ciencias biológicas como etología y biología evolutiva.
En ciencia política, dentro del campo de las relaciones internacionales, el escenario del dilema del prisionero se usa a menudo para ilustrar el problema de dos estados involucrados en una carrera armamentística. Ambos razonarán que tienen dos opciones: o incrementar el gasto militar, o llegar a un acuerdo para reducir su armamento. Ninguno de los dos estados puede estar seguro de que el otro acatará el acuerdo; de este modo, ambos se inclinarán hacia la expansión militar. La ironía está en que ambos estados parecen actuar racionalmente, pero el resultado es completamente irracional.
Otro interesante ejemplo tiene que ver con un concepto conocido de las carreras en ciclismo, por ejemplo el Tour de Francia. Considérense dos ciclistas a mitad de carrera, con el pelotón a gran distancia. Los dos ciclistas trabajan a menudo conjuntamente (cooperación mutua) compartiendo la pesada carga de la posición delantera, donde no se pueden refugiar del viento. Si ninguno de los ciclistas hace un esfuerzo para permanecer delante, el pelotón les alcanzará rápidamente (deserción mutua). Un ejemplo visto a menudo es que un sólo ciclista haga todo el trabajo (coopere), manteniendo a ambos lejos del pelotón. Al final, esto llevará probablemente a una victoria del segundo ciclista (desertor) que ha tenido una carrera fácil en la estela del primer corredor.
Un ejemplo adicional se puede observar en las intersecciones de dos vías por donde circulan autos y donde ninguna tiene una preferencia sobre la otra: si todos los conductores colaboran y hacen turnos para pasar, la pequeña espera se justifica por el beneficio de no generar una congestión en el medio. Si alguien no colabora y el resto sí, se beneficia el «no colaborador» generando un desorden en la secuencia de turnos que perjudica a los que estaban colaborando. Por último, cuando nadie quiere colaborar y tratan de pasar primero, se genera una gran congestión donde todos pierden mucho tiempo.
Una variante de éste juego especialmente útil para justificar la afirmación de que los principios de justicia se explican a través de la teoría de juegos y la evolución, es el juego llamado “Dilema del prisionero iterado”.
Esta variante del juego se produce cuando los prisioneros no juegan una sola vez el juego, sino que lo juegan varias veces, de forma sucesiva y con memoria. Ahora los participantes en el juego repiten el mismo varias veces, y lo que es mejor, se acuerdan de si en la partida anterior su contrincante les traicionó o cooperó.
Tal y como mostró el premio nobel Robert Aumann en 1959, si el juego del prisionero se juega repetidamente y con memoria un número indefinido de veces el resultado es que los jugadores acaban estableciendo una estrategia de cooperación.
Mediante competiciones reales y simulaciones por ordenador se ha determinado que en éste juego del prisionero iterado el egoísmo no es rentable, la mejor estrategia para ganar en el juego es la llamada de “venganza sin rencor” o “Tit for Tat with forgiveness.» (“Donde las dan las toman con capacidad de perdón”).
La estrategia ganadora es simple: En la primera jugada cooperaremos y, a partir de ahí, haremos lo que haya hecho el oponente en la jugada anterior; si nos traiciona le traicionaremos, si coopera entonces cooperaremos. Como la estrategia puede conducir a un bucle si nuestro adversario aplica la misma estrategia, en algunas pocas ocasiones, olvidaremos su traición y cooperaremos. Finalmente los estudios demuestran que ambos contendientes acaban cooperando y que la estrategia más egoísta es, precisamente, la altruista. Desde un punto de vista egoísta lo más aconsejable precisamente es, paradójicamente, establecer una conducta altruista.
Quedémonos, pues, con esta paradoja aparente pues en los capítulos siguientes volveremos sobre ella.
Marvin Minsky, uno de los padres de la inteligencia artificial, fue un científico que dedicó mucho tiempo al estudio de la mente humana y llegó a llamar al ser humano «The Emotion Machine» (La Máquina de las Emociones) porque entebdió que, en la base de todo comportamiento humano y en la base de su proceso de toma de decisiones se encontraban estas aplicaciones de programación de comportamientos desarrolladas por la evolución a las que llamamos emociones. Incluso propugnó que, si habíamos de diseñar una máquina inteligente, habríamos de dotarla de emociones pues son un recurso absolutamente genial para economizar y administrar eficazmente los escasos recursos de que disponen los seres vivos. Si un león nos ataca nuestro organismo disparará la emoción llamada «miedo» y, a partir de ese momento, todos los recursos de nuestro organismo se destinarán a correr como alma que lleva el diablo; si lo piensan un gran invento de la evolución.
Es importante entender el papel que juegan las emociones en la toma de decisiones por parte de los seres humanos y antes de pasar a estudiar estrategias complementarias de la reciprocidad —según les prometí en el capítulo anterior— creo que es necesario dedicar un poco de tiempo a estudiar, aunque sea de forma somera, el papel que juegan las emociones en nuestra vida.
Si observamos el comportamiento de los seres humanos en la vida cotidiana no nos costará descubrir en cuántas ocasiones las emociones determinan sus conductas. No necesito contarles cómo la naturaleza se encarga de que los padres sientan por sus hijos un amor (una poderosa emoción ¿verdad?) tan acrítico e indisimulado —sobre todo en sus primeros años de vida— que los ven los seres más hermosos del universo; y no se empeñe usted en discutir eso con una madre o un padre porque, aunque le reconozcan en un conato de lucidez que todos los niños son iguales, sus hijos, en su mirada y su mente, son únicos y es una de esas causas por las que mujeres y hombres se trasmutan. El amor paternofilial es una de esas emociones que hacen que un ser humano dé la vida por otro y eso padres y madres lo saben muy bien.
Tampoco necesito contarle tampoco cómo ese afolescente feo, canijo y poco agraciado, del que su hija se ha enamorado es para ella el ser más adorable del mundo y cómo, aunque sea un majadero notable, ella juzgará cualquier idiotez suya como una gracia y hasta le parecerá artística la roña de sus tobillos, las espinillas grasientas de su cara o la pelusa mal afeitada de su barba adolescente. Es el amor otra vez, sí, las emociones como esta o como la de paternidad/maternidad cambian en las perdonas hasta la forma en que ven el mundo.
Los seres humanos (y en general todos los animales) venimos al mundo con un complejo equipamiento de emociones que dirigen nuestras vidas y muchas de estas emociones tienen trascendencia jurídica. Ya vimos que la reciprocidad está en la base de la cooperación y por eso no le extrañará que los seres humanos dispongamos de emociones como la gratitud y la venganza o el rencor que nos estimulan a tratar con reciprocidad a aquellos individuos con los que interactuamos. Pero dejemos eso para más adelante, por ahora bástenos con tomar conciencia de cómo los genes dirigen o condicionan nuestras conductas a través de las emociones y las pasiones.
Es por todo esto que les contaba que Marvin Minsky, un científico que dedicó mucho tiempo al estudio de la mente humana, llegó a llamar al ser humano «The Emotion Machine» (La Máquina de las Emociones) porque en la base de todo su comportamiento y en la base de su proceso de toma de decisiones se encontraban estas aplicaciones de programación de comportamientos desarrolladas por la evolución a las que llamamos emociones.
Leí hace unos días en la red social «X» (antes tuíter) un micropost de un compañero abogado que decía textualmente:
El «Derecho Natural» no es el Derecho del Medioambiente, sino otra cosa más intangible y difícil de concretar: las leyes no escritas, dictadas por la recta razón o por Dios, que son perennes y válidas universalmente.
El micro post volvió a traerme a la mente uno de esos demonios que llevo a cuestas desde los tiempos de la universidad: el de la existencia o inexistencia de un conjunto de derechos universales —anteriores, superiores e independientes al derecho escrito, al derecho positivo y al derecho consuetudinario—, que llega a dar el fundamento a la obligatoriedad de la norma y que sirve de criterio para determinar la justicia o injusticia de una acción.
El micro post de mi compañero a la existencia de esas leyes no escritas les añadía un origen perturbador, al menos para mí, y es que estas leyes estarían dictadas por «la recta razón o por Dios».
Yo le respondí de forma más o menos velada que no estaba de acuerdo con tal origen y desde entonces me ronda la cabeza la idea de explicar en detalle cuál es mi visión de este asunto de forma que, ahora que dispongo de un rato libre, comenzaré y ya veremos luego cómo, cuándo y si termino.
Vamos al tajo.
Ni que decir tiene que, en un trabajo con pretensiones científicas, la hipótesis de un origen divino de estas normas debe ser descartada y la de que estas normas sean producto de la «recta razón» y no de procesos naturales es una hipótesis que, permítanme adelantárselo ya, por más que se encuentre extendida, carece a mi juicio de todo fundamento científico.
Y dicho lo anterior permítanme explicarme y justificar por qué entiendo que estas normas a las que llamamos «derecho natural» son un producto de procesos naturales que han determinado muchos de nuestros instintos y han conformado el criterio que permite a los seres humanos distinguir un hecho justo o moral de uno injusto o inmoral sin necesidad de haber cursado estudios jurídicos o de ética.
Y una vez dicho esto comencemos por el principio.
Gestionar el consentimiento de las cookies
Para ofrecer las mejores experiencias, utilizamos tecnologías como las cookies para almacenar y/o acceder a la información del dispositivo. El consentimiento de estas tecnologías nos permitirá procesar datos como el comportamiento de navegación o las identificaciones únicas en este sitio. No consentir o retirar el consentimiento, puede afectar negativamente a ciertas características y funciones.
Funcional
Siempre activo
El almacenamiento o acceso técnico es estrictamente necesario para el propósito legítimo de permitir el uso de un servicio específico explícitamente solicitado por el abonado o usuario, o con el único propósito de llevar a cabo la transmisión de una comunicación a través de una red de comunicaciones electrónicas.
Preferencias
El almacenamiento o acceso técnico es necesario para la finalidad legítima de almacenar preferencias no solicitadas por el abonado o usuario.
Estadísticas
El almacenamiento o acceso técnico que es utilizado exclusivamente con fines estadísticos. El almacenamiento o acceso técnico que se utiliza exclusivamente con fines estadísticos anónimos. Sin un requerimiento, el cumplimiento voluntario por parte de tu Proveedor de servicios de Internet, o los registros adicionales de un tercero, la información almacenada o recuperada sólo para este propósito no se puede utilizar para identificarte.
Marketing
El almacenamiento o acceso técnico es necesario para crear perfiles de usuario para enviar publicidad, o para rastrear al usuario en una web o en varias web con fines de marketing similares.
